• Java Program To Implement Circular Queue Adt Using An Array In Math Word
• Java Program To Implement Circular Queue Adt Using An Array In Math Pdf
• Java Program To Implement Circular Queue Adt Using An Array In Math Calculator

This article needs additional citations for. Unsourced material may be challenged and removed. (May 2009) In, an abstract data type ( ADT) is a for, where a data type is defined by its behavior from the point of view of a user of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations. This contrasts with, which are concrete representations of data, and are the point of view of an implementer, not a user. Formally, an ADT may be defined as a 'class of objects whose logical behavior is defined by a set of values and a set of operations'; this is analogous to an in mathematics.

What is meant by 'behavior' varies by author, with the two main types of formal specifications for behavior being axiomatic (algebraic) specification and an abstract model; these correspond to and of an, respectively. Some authors also include the ('cost'), both in terms of time (for computing operations) and space (for representing values). In practice many common data types are not ADTs, as the abstraction is not perfect, and users must be aware of issues like that are due to the representation. For example, integers are often stored as fixed width values (32-bit or 64-bit binary numbers), and thus experience if the maximum value is exceeded. ADTs are a theoretical concept in computer science, used in the design and analysis of algorithms, data structures, and software systems, and do not correspond to specific features of —mainstream computer languages do not directly support formally specified ADTs. However, various language features correspond to certain aspects of ADTs, and are easily confused with ADTs proper; these include, and. ADTs were first proposed by and Stephen N.

Zilles in 1974, as part of the development of the language. This section needs additional citations for. Unsourced material may be challenged and removed. (May 2011) Encapsulation provides a promise that any implementation of the ADT has certain properties and abilities; knowing these is all that is required to make use of an ADT object.

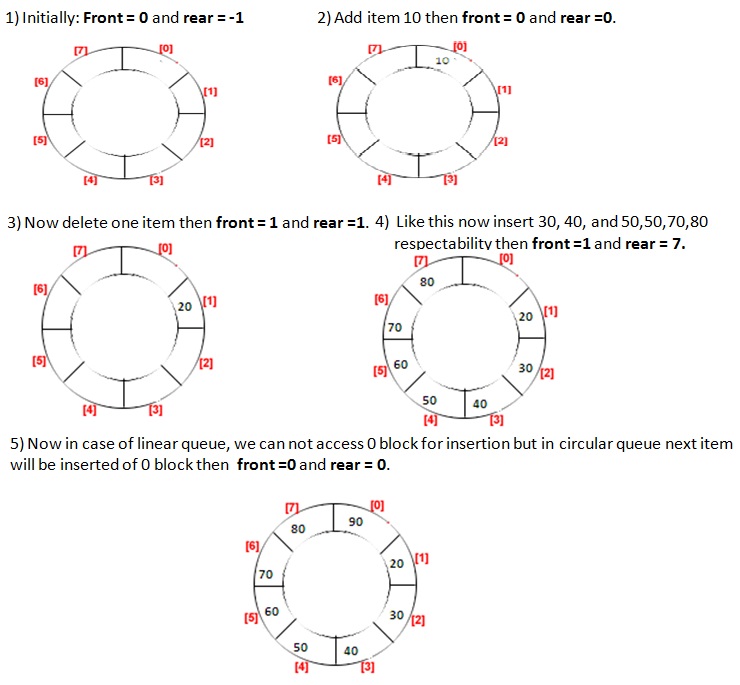
Topic: Implementation of Queue using Array in Data Structure Data and File Structure Complete Series Playlist: C Programming Complete P. Java Program To Implement Circular Queue Adt Using An Array Can Make A Program. STACK (ARRAY- BASED IMPLEMENTATION) (Java, C++). In computer science, an abstract data type (ADT) is a mathematical model for data types where a data type is defined by its behavior (semantics) from the point of view of a.

The user does not need any technical knowledge of how the implementation works to use the ADT. In this way, the implementation may be complex but will be encapsulated in a simple interface when it is actually used. Localization of change Code that uses an ADT object will not need to be edited if the implementation of the ADT is changed. Since any changes to the implementation must still comply with the interface, and since code using an ADT object may only refer to properties and abilities specified in the interface, changes may be made to the implementation without requiring any changes in code where the ADT is used.

Flexibility Different implementations of the ADT, having all the same properties and abilities, are equivalent and may be used somewhat interchangeably in code that uses the ADT. This gives a great deal of flexibility when using ADT objects in different situations. For example, different implementations of the ADT may be more efficient in different situations; it is possible to use each in the situation where they are preferable, thus increasing overall efficiency. Typical operations Some operations that are often specified for ADTs (possibly under other names) are.

compare( s, t), that tests whether two instances' states are equivalent in some sense;. hash( s), that computes some standard from the instance's state;. print( s) or show( s), that produces a human-readable representation of the instance's state. In imperative-style ADT definitions, one often finds also. create, that yields a new instance of the ADT;. initialize( s), that prepares a newly created instance s for further operations, or resets it to some 'initial state';.

copy( s, t), that puts instance s in a state equivalent to that of t;. clone( t), that performs s ← create, copy( s, t), and returns s;. free( s) or destroy( s), that reclaims the memory and other resources used by s. The free operation is not normally relevant or meaningful, since ADTs are theoretical entities that do not 'use memory'.

However, it may be necessary when one needs to analyze the storage used by an algorithm that uses the ADT. In that case one needs additional axioms that specify how much memory each ADT instance uses, as a function of its state, and how much of it is returned to the pool by free. Examples Some common ADTs, which have proved useful in a great variety of applications, are. Each of these ADTs may be defined in many ways and variants, not necessarily equivalent. For example, an abstract stack may or may not have a count operation that tells how many items have been pushed and not yet popped.

This choice makes a difference not only for its clients but also for the implementation. Abstract graphical data type An extension of ADT for computer graphics was proposed in 1979: an (AGDT). It was introduced by, and. Left behind eternal forces patch. AGDTs provide the advantages of ADTs with facilities to build graphical objects in a structured way.

Implementation. Further information: Implementing an ADT means providing one for each abstract operation. The ADT instances are represented by some concrete that is manipulated by those procedures, according to the ADT's specifications. Usually there are many ways to implement the same ADT, using several different concrete data structures. Thus, for example, an abstract stack can be implemented by a or by an. In order to prevent clients from depending on the implementation, an ADT is often packaged as an in one or more, whose interface contains only the signature (number and types of the parameters and results) of the operations.

Java Program To Implement Circular Queue Adt Using An Array In Math Word

Java Program To Implement Circular Queue Adt Using An Array In Math Pdf

Java Program To Implement Circular Queue Adt Using An Array In Math Calculator

The implementation of the module—namely, the bodies of the procedures and the concrete data structure used—can then be hidden from most clients of the module. This makes it possible to change the implementation without affecting the clients. If the implementation is exposed, it is known instead as a transparent data type. When implementing an ADT, each instance (in imperative-style definitions) or each state (in functional-style definitions) is usually represented by a of some sort. Modern object-oriented languages, such as and, support a form of abstract data types.

When a class is used as a type, it is an abstract type that refers to a hidden representation. In this model an ADT is typically implemented as a, and each instance of the ADT is usually an of that class. The module's interface typically declares the constructors as ordinary procedures, and most of the other ADT operations as of that class.

However, such an approach does not easily encapsulate multiple representational variants found in an ADT. It also can undermine the extensibility of object-oriented programs. In a pure object-oriented program that uses interfaces as types, types refer to behaviors not representations. Example: implementation of the abstract stack As an example, here is an implementation of the abstract stack above in the. Imperative-style interface An imperative-style interface might be.